数据结构:红黑树
概述
红黑树的性质:
- 节点或是红色,或是黑色;
- 根节点是黑色;
- 叶节点(NIL)是黑色;
- 如果一个节点是红色,那么它的两个孩子都是黑色;
- 对任一节点,从该节点到叶节点的所有简单路径上包含相同数目的黑色节点。
添加节点
除了需要做红黑树性质的维护,红黑树的插入算法和普通的二叉树插入算法是一致的。
节点 x 插入之后,如果 x 的父节点是红色的,这时需要做红黑调整,否则节点添加结束。
以下只考虑 x 的父节点是左孩子的情况,父节点为右孩子时,对称处理。
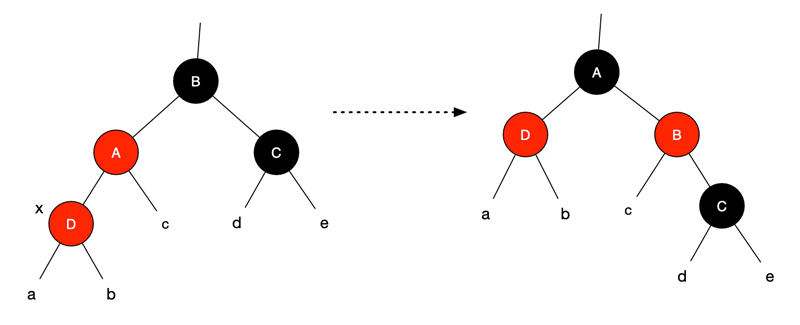
1. 叔节点是红色(左右一致)
此时,A、C、D 是红色,B 为黑色。目标:x 上移 2 层,指向爷爷节点 B。
填充 A、C 为黑色,B 为红色,x 指向节点 B。如果 B 的父节点为黑色,问题解决;否则继续下一轮。
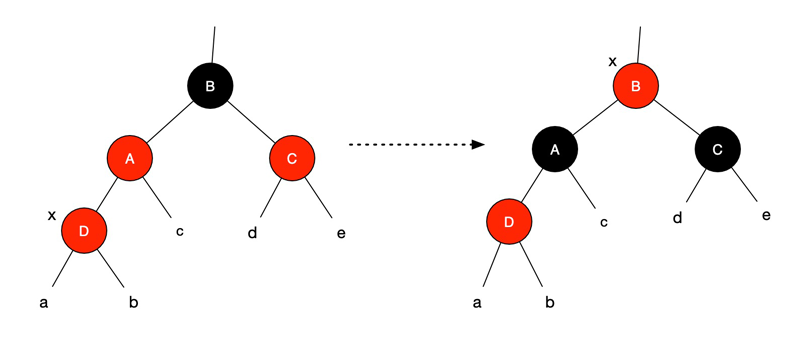
2. 叔节点是黑色,x 是右孩子
此时,A、D 为红色,B、C 为黑色。目标:把 x 节点调整成左孩子。
对 D 子树做左旋操作,x 指向原先的父节点 D。
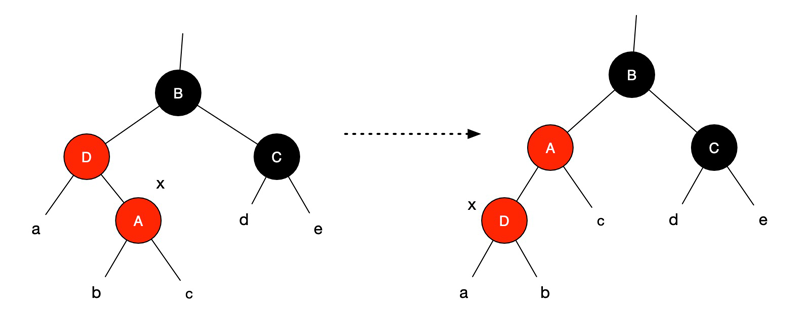
3. 叔节点是黑色,x 是左孩子
此时,A、D 为红色,B、C 为黑色。目标:调整完毕。
交换 A、B 的颜色,对 B 子树做右旋操作,问题解决。
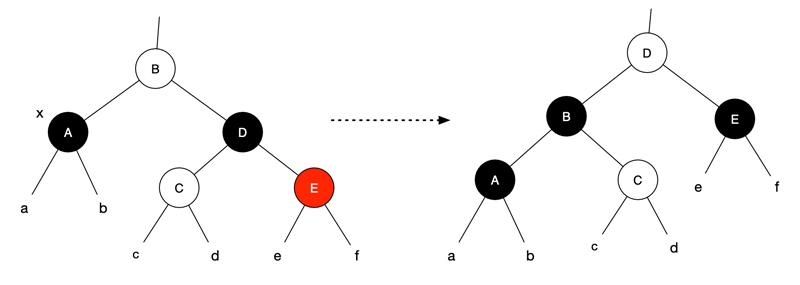
删除节点
下面是在红黑树中删除一个节点的大概流程,其中:z 为待删除节点;y 要么指向 z,要么指向 z 的直接后继节点;x 指向 y 的右孩子或者左孩子。
- y 初始化指向 z;
- 如果 z 没有左孩子,直接用右子树顶替 z,x 指向 z 右孩子;
- 如果 z 没有右孩子,直接用左子树顶替 z,x 指向 z 左孩子;
- 如果 z 孩子双全,使用 z 的直接后继 y 替换 z;
- 此时,y 位于 z 右子树的最左侧,没有左孩子,x 指向 y 可能的右孩子;
- 如果 y 不是 z 的右孩子,用 y 的右子树替换 y 子树;
- y 移动到 z 的位置;
- y 填充 z 的颜色,节点删除完成。
如果 y 本身是黑色,不管是它被删除,还是从原来的位置移动到 z 的位置,都会导致原先的 y 子树,也就是现在的 x 子树少 1 个黑色,因而部分祖先节点可能会违反性质 5。
我们把少掉的这一个黑色临时放在 x 节点上,也就是 x 具有双重颜色,红-黑,或者,黑-黑,由于 x 多贡献一个黑色,性质 5 也就被满足了。接下来要做的是把这多出来的一个黑色在 x 的祖先节点上移动,找出一个合适的节点给他填充上,问题就解决了。
如果 x 是根节点,可能会违背性质 2,直接给填充黑色,问题解决;如果 x 是红色,填充黑色,问题解决;如果 x 是黑色,根据 x 是左孩子、右孩子分别有四种情况。
以下只考虑 x 是左孩子的情况,为右孩子时,对称处理。 注意,在整个处理过程当中,x 指向的节点具有双重颜色。
1. 兄弟是红色
此时,x 的父节点 B 必定为黑色,C 和 E 必定为黑色。目标:x 拥有黑色的兄弟节点。
交换 B 和 D 的颜色,并对以 B 为根的子树做左旋操作。完了之后,x 的父节点 B 成了红色,兄弟为原来兄弟 D 的左孩子,肯定是黑色。红黑树的各项性质依然保持,继续 2、3、4 之一。
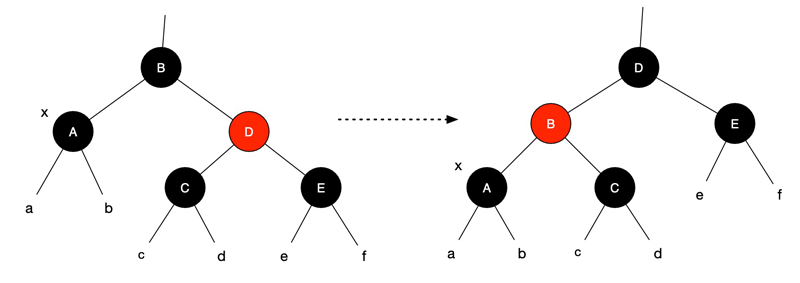
2. 兄弟是黑色,其左右孩子均为黑色
此时父节点 B 颜色随意,A、C、D、E 均为黑色。目标:x 指向父节点。
上移 x 多出的黑色和兄弟节点 D 的黑色给父节点 B,填充兄弟节 D 点为红色,x 指向父节点 B。此时 x 为红-黑或黑-黑,红黑树性质依然保持。
若 x 为红-黑,也就是说节点 B 原来为红色,填充 x 为黑色,问题解决;否则继续走下一轮。
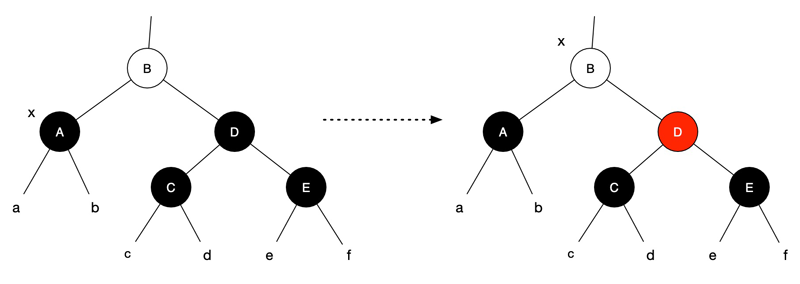
3. 兄弟是黑色,其左孩子为红色,右孩子为黑色
此时父节点 B 颜色随意,A、D、E 为黑色,C 为红色。目标:x 的黑色兄弟拥有红色的右孩子。
对以 D 为根的子树做右旋操作,并交换 C、D 的颜色,红黑性质依然保持,继续第 4 步。
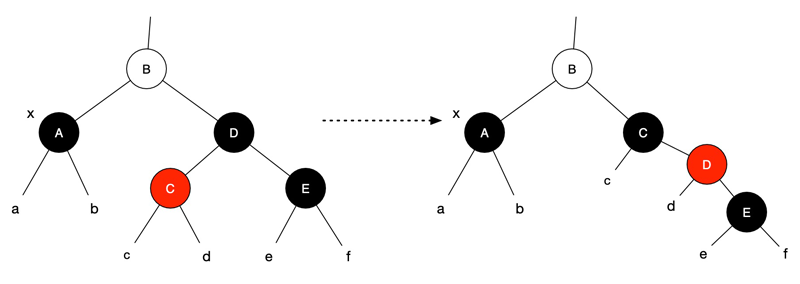
4. 兄弟是黑色,其左孩子随意,右孩子为红色
此时,A、D 为黑色,E 为红色,B、C 颜色随意。目标:问题解决。
D 的黑色给到 E,B 的颜色给到 D,A 多出来的黑色给到 B,以 B 为根节点执行左旋操作,问题解决。